Team 12: Nick Morgan, Antolín Moral Caballero, and Yejin Eun¶
Table of Contents¶
- Problem statement and motivation
- Introduction and description of data
- A revised project workflow based on the insights from EDA
- Data wrangling prior to EDA
- Exploratory Data Analysis
- Literature review / related work
- Modeling approach and project trajectory
- Results
- Conclusions and Future Work
Note: We have hidden most of the code in the notebook and displayed important cells for better readability.
Problem statement and motivation¶
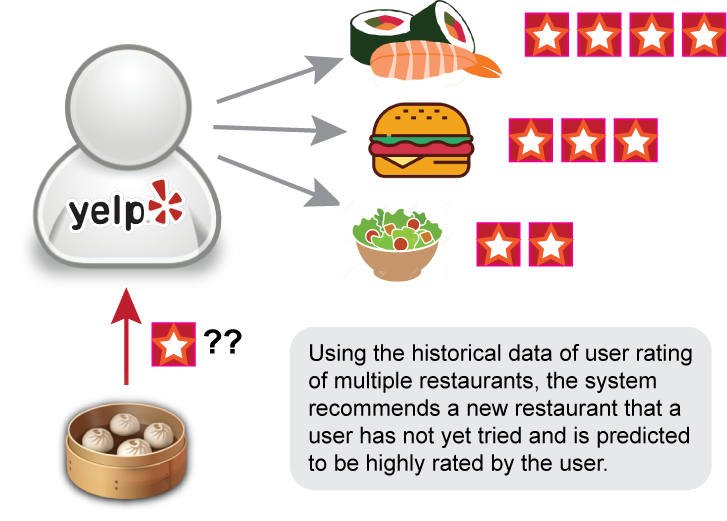
Using user review data from Yelp, our aim was to develop a recommendation system to provide a new restaurant suggestion that a user might like. The project was motivated by the fact that recommendation problems are ubiquitious, including the infamous Netflix challenge and "similar items you might like" suggestions from Amazon. Given the diverse application of this problem, we wanted to learn how to develop and implement such system using machine learning. Below, we graphically illustrate our project goal.
Introduction and description of data¶
 Image credit: Yelp
Image credit: Yelp
The Yelp data is vast and rich: it contains millions of reviews of different business types (e.g. restaurants and dry cleaners), and each business type has different set of attributes associated with them. Each review at minimum consists of review text and review star rating. Because of its size and richness, it presented an initial challenge for us to decide what data to include in our modeling and what features should be engineered. In addition, not every user has made several reviews or reviews with different ratings, so we needed to figure out what datasets to use for training vs. testing. To this end, we performed EDA on the data, specifically to look at relevant business attributes, user attributes, and reviews. We reasoned that these are the core information needed to link users and businesses with their preferences (hence, we disregarded data such as checkin, photos, and tip).
A revised project workflow based on the insights from EDA¶
We will use the cleaned datasets to accomplish three major goals:
- Create a baseline estimate of a rating. This simple model will be created by recording the biases of each user and item to make a baseline estimate of a given user-item combination.
- Create a regularized regression to improve the accuracy of our baseline model.
- Use a Neighborhood model based on a item-to-item approach as a method of collaborative filtering to improve our model further. Our initial Neighborhood model will not include features of the restaurant, but rather, similarities between restaurants based on the users that have reviewed it.
Data wrangling prior to EDA¶
Converting JSON files to CSV¶
We downloaded a 5.6 GB TAR file from Yelp. This TAR file contained second TAR file that we extracted to get a series of JSON files: business, checkin, photos, review, tip, and user. Pandas has a read_json function, but it returned a Trailing Data Error when used on these specific files. As a result, we created a Python script that converts these JSON files into CSV files.
def json_to_csv(directory, fileNames, createSample=False):
"""
json_to_csv: loops through specified JSON files and converts them to csv files.
option to also create a sample csv, which uses np.random.seed 9001 to create a sample dataset with 10% of the observations
pandas has a read_json function, but returns a 'Trailing data error' when working with these specific files
Inputs: -directory of JSON files
-list of JSON filenames
-createSample flag
"""
start = time.time()
jsonData = []
for fileName in fileNames:
with open(directory + fileName, encoding="utf8") as file:
print('{0} opened'.format(fileName))
for line in file:
#I use an rstrip here because some of the files have trailing blank spaces
jsonData.append(json.loads(line.rstrip()))
df = pd.DataFrame.from_dict(jsonData)
csvFileName = fileName[:len(fileName)-5] + '.csv'
df.to_csv(directory + csvFileName)
print('{0} created'.format(csvFileName))
if createSample:
np.random.seed(9001)
msk = np.random.rand(len(df)) <= 0.1
sample = df[msk]
csvSampleFileName = fileName[:len(fileName)-5] + '_sample.csv'
sample.to_csv(directory + csvSampleFileName)
print('{0} created'.format(csvSampleFileName))
print('This function took {} minutes to run'.format((time.time()-start)/60))
Keeping only "restaurant" business data and other associated data on users and reviews¶
We reduced the business dataset to businesses that had “Restaurant” or “Food” in the category (restaurants). We then removed observations that had other “non-restaurant” categories, such as “Grocery”, “Auto Glass Services”, “Business Consulting”, etc. After reducing the business dataset, we reduced our review dataset in two ways:
- Only including reviews for businesses that existed in the reduced business (restaurant) dataset
- Only including reviews for users that have at least 2 reviews (A single rating does not help determine similarities between restaurants)
In summary, we began with 156,639 observations. 15,502 of these observations contained "Food" or "Restaurants". After removing observations with irrelevant categories, we are left with 14,032 total observations.
Number of businesses that have both "food" and "restaurant" in their category:
# create a mask for restaurants
mask_restaurants = business['categories'].str.contains('Restaurants')
# create a mask for food
mask_food = business['categories'].str.contains('Food')
# apply both masks
restaurants_and_food = business[mask_restaurants & mask_food]
# number of businesses that have food and restaurant in their category
restaurants_and_food['categories'].count()
Even after taking buisnesses that have both food and restaurant in their categories, there are still irrelevant business categories in the data.
# an example row
restaurants_and_food.head(1)['categories'].values
Thus, we manually identified additional categories that needed to be excluded specifically.
categoriesToRemove = ['Grocery','Drugstores','Convenience Stores','Beauty & Spas','Photography Stores & Services',
'Cosmetics & Beauty Supply','Discount Store','Fashion','Department Stores','Gas Stations',
'Automotive','Music & Video','Event Planning & Services','Mobile Phones','Health & Medical',
'Weight Loss Centers','Home & Garden','Kitchen & Bath','Jewelry',"Children's Clothing",
'Accessories','Home Decor','Bus Tours','Auto Glass Services','Auto Detailing',
'Oil Change Stations', 'Auto Repair','Body Shops','Car Window Tinting','Car Wash',
'Gluten-Free','Fitness & Instruction','Nurseries & Gardening','Wedding Planning',
'Embroidery & Crochet','Dance Schools','Performing Arts',
'Wholesale Stores','Tobacco Shops','Nutritionists','Hobby Shops','Pet Services',
'Electronics','Plumbing','Gyms','Yoga','Walking Tours','Toy Stores','Pet Stores',
'Pet Groomers','Vape Shops','Head Shops',
'Souvenir Shops','Pharmacy','Appliances & Repair','Wholesalers','Party Equipment Rentals',
'Tattoo','Funeral Services & Cemeteries','Sporting Goods','Dog Walkers',
'Pet Boarding/Pet Sitting','Scavenger Hunts','Contractors','Trainers',
'Customized Merchandise', 'Dry Cleaning & Laundry', 'Art Galleries'
'Tax Law', 'Bankruptcy Law', 'Tax Services', 'Estate Planning Law',
'Business Consulting', 'Lawyers', 'Pet Adoption', 'Escape Games',
'Animal Shelters', 'Commercial Real Estate', 'Real Estate Agents',
'Real Estate Services', 'Home Inspectors']
Expanding business attributes & categories¶
After cleaning the business dataset, we expanded the attributes into boolean features. The attributes were a collection of a string of a dictionary. We evaluated this string as a dictionary and applied pd.Series across the result, which expanded this dictionary into multiple Boolean columns, as well as a few more dictionary columns. All remaining dictionary columns were manipulated in the same manner, leaving us ~70 Boolean columns. The business dataset also had a variable, categories, that was a string of a list. We expanded this list into separate columns for each category. Lastly, we then reduced our user dataset by filtering to users that existed in the reduced review dataset. The following functions were used for this process.
#create_attributes
#takes a dataframe as an input, as well as a list of columns that are dictionaries
#takes each column that is a dictionary, and expands it into a series of dummy columns
def create_attributes(df, dictList):
for dictionaryColumn in dictList:
#the attributes column is a string of dictionaries, so one extra step is taken to convert
if dictionaryColumn == 'attributes':
expandedColumns = df[dictionaryColumn].map(eval).apply(pd.Series)
else:
expandedColumns = df[dictionaryColumn].apply(pd.Series)
df = pd.concat([df.drop(dictionaryColumn,axis=1),
expandedColumns]
,axis=1)
#df.fillna(value='{}',inplace=True)
return df
def expand_categories(df, cat_var, key):
all_cats = df[cat_var].str.cat(sep=', ')
all_cats = all_cats.replace('[', '')
all_cats = all_cats.replace(']', '')
all_cats = all_cats.replace("\'","")
all_cats = all_cats.replace('"','')
all_cats_list = all_cats.split(', ')
unique_cats = list(set(all_cats_list))
unique_cats.remove('Restaurants')
unique_cats.remove('Food')
df_cats = pd.DataFrame(index=df[key], columns=unique_cats, data=False)
df_out = df.merge(df_cats, how='left', left_on=key, right_index=True)
for cat in unique_cats:
df_out[cat] = df_out[cat_var].str.contains(cat)
return df_out
Before expansion:
restaurants_df.head(1)
After expansion:
expanded.head(1)
After cleaning up the business data, we kept relevant review and user data only.
def reduce_review(df, business_list):
#drop columns where business_id or user_id is null
df.dropna(subset=['business_id','user_id'], how='any',inplace=True)
#restrict to businesses that are restaurants
df = df[df['business_id'].isin(business_list)]
#only keep user_id's with more than one review
df = df[df.groupby('user_id').user_id.transform(len) > 1]
#verify this worked by taking the minimum amount of user_id counts
print('The minimum amount of reviews per user is {}'
.format(np.min(df.groupby('user_id')['business_id'].count())))
return df
restaurant_reviews.head()
users_w_reviews.head(1)
Then we finally merged all cleaned DFs.
recommendations.head()
Exploratory Data Analysis¶
Most users have only a few number of reviews.¶
Most users have only 1, 2 or 3 reviews (90% of users have less than 10 reviews) and the average stars per user (including all type of business, not restricted to restaurants) is 3.75. This indicates that a final matrix with users and businesses will be a sparse matrix. It may be difficult to give recommendations to users that don’t review many restaurants, especially if those restaurants don’t have many reviews. Further, there are 2,373 users that rate everything as 1, which will make recommendations difficult as we do not have data of anything they like so we won’t make recommendations for those users.
num_reviews_per_var(reviews, 'user_id', 'review_id', 20, 'num_reviews', '% of users')
User bias: some users tend to give higher ratings than others.¶
The histogram also shows differences in the average stars per user showing that some users tend to give higher ratings than others. These biases between users will be captured by our baseline model.
fig, ax = plt.subplots(1,1, figsize=(7, 6))
users[y_user].plot(kind='hist', ax=ax)
ax.set_xlabel('Users Average Stars')
plt.show()
Most businesses have more than 3 reviews.¶
Looking at business, the distribution of number of reviews per business is less ‘right-skewed’ and we have more restaurants with more than 3 reviews.
num_reviews_per_var(reviews, 'business_id', 'review_id', 20, 'num_reviews', '% of business')
Reducing the number of business categories¶
After expanding the business categories, we ended up with a dataframe of ~460 columns where each column was a distinct category. This number is too large, and we had to select categories that were more relevant to the goal of making recommendations to users. To find out which categories are most prominent and which are relevant for restaurant recommendation, we first got rid of the categories that only occur a few times in the dataset (the cutoff used was 11). These tended to be the ones not relevant to restaurants. Looking at the top 10 and bottom 10 categories in terms of number of occurrences, we found that the top 10 are mostly fast food or quick food places, and the bottom 10 are mostly ethnic food places. This gave us the idea that if two users like some of these rarely occurring restaurant categories, perhaps we could give them a greater weight when predicting/recommending the next restaurant.
fig, ax = plt.subplots(1, 2, figsize=(15, 5))
sns.barplot(x='count', y='category', data=num_busi_cat.head(10), color='lightgrey', ax=ax[0])
ax[0].set(ylabel='restaurant category')
ax[0].set(xlabel='number of occurance')
ax[0].set(title='Top 10 restaurant categories')
sns.barplot(x='count', y='category', data=num_busi_cat.tail(10), color='lightgrey', ax=ax[1])
ax[1].set(xlabel='number of occurance')
ax[1].set(title='Bottom 10 restaurant categories')
ax[1].set(ylabel='')
plt.tight_layout()
plt.show()
Restaurant categories can be further reduced to a smaller set of dimensions.¶
After getting rid of the categories that only occur a few times in the dataset, we still had ~180 restaurant categories. While this number is smaller than the original we started with (~460), we sought to further reduce the number by performing dimensionality reduction (specifically, PCA). By doing so, we obtained the first 30 principal components that explained ~75% of the total variance in the data. Looking at the first 3 PCs for visualization, we found that the top three categories (fast food, sandwiches, and coffee & tea) are nicely clustering in these spaces. Given these results, we think that dimensionality reduction could be a useful way to incorporate many features related to restaurants for finding similar restaurants in the recommendation system.
feature_name = 'Fast Food'
plot_pca_results(0, 1, feature_name)
feature_name = 'Sandwiches'
plot_pca_results(1, 2, feature_name)
feature_name = 'Coffee & Tea'
plot_pca_results(0, 1, feature_name)
Exploring the relationship between different restaurant attributes/categories:¶
We explored the relationship between different attributes so that it would help us further narrow down the list of attributes we would keep for collaborative filtering. We found that higher the restaurant price range, more restaurants have dressy/formal attire attributes. Also higher the price range, more restaurants accept reservations. Given these relationships, we could eliminate reservation acceptance and attire features, and keep only the price range feature. In a similar manner, we found that the diversity of alcohol served and whether the restaurant is good for kids were negatively related (visualization not shown here), suggesting that only one of these features is needed due to their interaction.
temp = makePercPivotTable('RestaurantsPriceRange2', 'RestaurantsAttire', 'OutdoorSeating')
temp = temp[temp['RestaurantsPriceRange2']!='unknown']
temp = temp[temp['RestaurantsAttire']!='unknown']
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
sns.pointplot(x='RestaurantsPriceRange2', y='perc', hue='RestaurantsAttire',
data=temp,
palette='Blues', ax=ax)
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set(xlabel='restaurant price range')
ax.set(ylabel='restaurant attire, % of each price range')
ax.set(title='relationship of price and attire')
plt.show()
temp = makePercPivotTable('RestaurantsPriceRange2', 'RestaurantsReservations', 'OutdoorSeating')
temp = temp[temp['RestaurantsReservations']!='unknown']
temp = temp[temp['RestaurantsPriceRange2']!='unknown']
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
sns.pointplot(x='RestaurantsPriceRange2', y='perc', hue='RestaurantsReservations',
data=temp, hue_order=[False, True],
palette='RdBu' , ax=ax)
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set(xlabel='Restaurant price range')
ax.set(ylabel='% of whether reservations are taken')
ax.set(title='relationship of reservaton option and price range')
plt.show()
On the other hand, the noise level of restaurants and whether it’s a good place for groups or it has a TV did not seem to have a strong positive or negative relationship.
temp = makePercPivotTable('HasTV', 'NoiseLevel', 'OutdoorSeating')
temp = temp[temp['HasTV']!='unknown']
temp = temp[temp['NoiseLevel']!='unknown']
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
sns.pointplot(x='HasTV', y='perc', hue='NoiseLevel',
data=temp, hue_order=['quiet', 'average', 'loud', 'very_loud'],
palette='Blues', ax=ax)
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set(xlabel='Has TV')
ax.set(ylabel='% of noise category')
ax.set(title='relationship of TV presence and noise')
plt.show()
Exploring the relationship between user attributes and the avg. star rating of a user¶
For this purpose, we created 3 new features from the original features in the dataset:
- User_friends_flag that indicates if the user has at least one friend
- User_elite_flag that indicates if the user has been an “elite user” at least one
- The year since when the user is at Yelp
The 2 first features seemed to have some relationship with the average number of stars of the user but the year does not seem to be a factor. Other features from the user dataset has been explored but they did not seem to have a significant relationship with the avg. star rating.
fig = plt.figure(figsize=(12, 10))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222)
# f, ax = plt.subplots(1, 2, figsize=(10, 4))
g = sns.factorplot(x="user_friends_flag", y=y_user, data=users, kind='bar', ax=ax1);
ax1.set_ylim(3, 4);
plt.close(g.fig);
g = sns.factorplot(x="user_elite_flag", y=y_user, data=users, kind='bar', ax=ax2);
ax2.set_ylim(3, 4);
plt.close(g.fig);
plt.show();
Literature review / related work¶
1. Creating a baseline model¶
Before trying collaborative filtering which is based on user's experience with a particular restaurant, we first created a baseline model that captures the user's bias (e.g. some users are more likely to give higher ratings than others) and the bias of the restaurant (e.g. a restaurant could be a part of a national chain like Cheesecake Factory that has a higher brand power than Chipotle that recently suffered from mass infections). To this end, we relied on the method described in Advances in Collaborative Filtering, (link) by Yehuda Koren's and Robert Bell.
2. Collaborative filtering¶
Collaborative filtering is based on the past experience of a user with different restaurants so that we can find what new restaurants that are similar to the ones user liked in the past for recommendation, and also to find the new restaurants that similars users have liked already. We found the following two websites very useful for understanding the concepts and methods for implementation (i.e. singular value decomposition and cosine similarity through pairwise distances).
Modeling approach and project trajectory¶
I. Baseline modeling¶
Using the method described in Advances in Collaborative Filtering, (link) by Yehuda Koren's and Robert Bell, we created a baseline model with user bias and restaurant bias terms. According to Koren and Bell, the baseline model can be expressed as the following:
$b_{u i} = \mu + b_{u} + b_{ i}$
where $\mu$ represents the mean of all ratings. $b_{u}$ and $b_{i}$ represent the observed deviation of user $u$ and item $i$, respectively. In order to find the parameters $b_{u}$ and $b_{i}$, we used two approaches:
Approach 1: Use the formulas given in the Koren and Bell paper to find the bias¶
Where $\lambda_{2}$ and $\lambda_{3}$ are the regularization parameters (to be chosen by cross-validation), R(i) represents all users who rated item $i$, and R(u) represents all items that user $u$ has rated.
Approach 2: Use Ridge regression to find the bias terms¶
We performed Ridge Regression using cross-validation.
II. Memory-Based Collaborative filtering¶
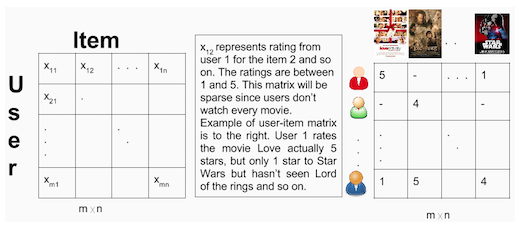
As noted above in the Literature section, we wanted to take advantage of the wide user base and restaurant rating history in the Yelp database to provide a better recommendation system than the baseline model. To this aim, we implemented collaborative filtering (CF). The first step of CF is to create a user-item matrix, such as the one shown here for users and movies (image credit: CF ref 1).
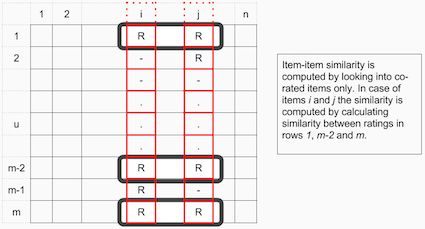
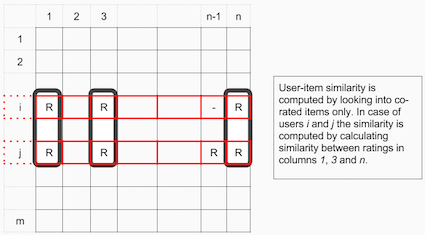
Using this user-item matrix, we can calculate the similarities between two items, and also between two users. Between two items, we are looking to find how their ratings were similar. For user-user similarity, we look at all the items that were commonly rated by the two users and how much their ratings were similar. By doing so, we obtain similarity metrics for item-item and user-user, leading to item-item collaborative filtering and user-item collaborative filtering, respectively. These concepts are nicely illustrated in the following images (image credit: CF ref 2).
Item-Item collaborative filtering will measure similarity by observing all users who have rated both restaurants.
User-Item collaborative filtering will measure similarity by observing all items that are rated by both users.
To calculate the similarity, we used cosine similarity. We consider the ratings as vectors in n-dimensional space, and calculate the angle between these vectors to determine the similarity. Cosine similarity for users a and m are calculated using the following formula:
Because the Yelp ratings are in the scale of 1-5 (all positive numbers), the output of cosine distance will range between 0 and 1, where a value closer to 1 means a higher similarity.
III. Model-Based Collaborative filtering¶
Because there is not a huge overlap between all users and all restaurants, we observed that our dataframe is very sparce (>99.9%), as expected. Given this sparsity, we also implemented model-based CF that is able to deal with sparsity better than memory-based CF. Other drawbacks to memory-based CF include 1) lack of scalability and 2) cold-start problem. Cold-start problem means that it is not possible to make predictions for new users or restaurants that has no previous rating at all. Model-based collaborative filtering can handle higher sparsity levels and is more scalable, but also suffer from the cold-start problem.
The way the model-based collaborative filtering handles high sparsity is through dimensionality reduction and latent variable decomposition. Although we only have the users' ratings for businesses as the dataset, underlying this data are the hidden preferences of users for certain businesses because of their hidden attributes. These latent variables are learned by the model-based CF. To do this, we used matrix factorization, which provides the latent vectors and allows filling in the sparse, original matrix: it predicts unknown ratings by taking the dot product of the latent features of users or items. For implementing matrix factorization, we used singular value decomposition (SVD). SVD is solved as follows:
$$X = U * S * V^{(T)} $$Where:
- X represents an m x n matrix
- U represents the m x r orthogonal matrix
- S represents the r x r diagonal matrix with non-negative real numbers on the diagonal
- $V^{(T)}$ represents the r x n orthogonal matrix
- Elements on the diagonal of S are known as singular values of X
Matrix X can be factorized into U, S, and V.
- U represents the feature vectors corresponding to users in the hidden feature space
- V represents the feature vectors corresponding to items in the hidden feature space
Finally, we make our prediction by taking the dot product of U, S, and $V^{(T)}$.
IV. Model evaluation¶
To maintain compatibility with results published by others implementation of recommendation systems, we are going to adopt the standard set by the Netflix prize and the quality of our results will be measured using the root mean squared error (MSE).
$${\mathit{R}\mathit{M}\mathit{S}\mathit{E}} = \sqrt{\frac{1}{N}\sum(x_{i} - \hat{x_{i}})^{2}}$$That measure puts more emphasis on large errors compared with the alternative of mean absolute error.
V. Decisions from the modeling¶
We found that the model-based CF had the lowest RMSE on the test set, thus we decided to pursue this approach for the recommendation system. We observed that for this model, the RMSE of validation data does not change too much for different values of k (i.e. at all values of k we tested, the RMSE is lower than other models by a factor of 10 or more). Thus, we decided to go with a large k (i.e. 100) so that we can make a greater number of predictions.
The baseline model¶
Approach 1: Obtain user and restaurant bias by using formulas given by Koren and Bell.¶
For this approach, we created the next two functions. Using these functions, we looped through possible user bias and restaurant bias values, and used cross-validation to determine which combination is optimal.
def get_restaurant_offsets(df, rating, bus_id, bus_avg, lambda2):
overall_avg = df[rating].mean()
#top of equation
df['individualRatingMinusAverage'] = df[rating] - overall_avg #temporary column
summedDifference = df.groupby(bus_id)['individualRatingMinusAverage'].sum()
df.drop('individualRatingMinusAverage',axis=1,inplace=True) #get rid of temporary column
#bottom of equation
ratingCount = df.groupby(bus_id)[rating].count()
#final result
bias = pd.DataFrame(data=summedDifference / (ratingCount + lambda2),
columns=['business_bias'])
#add result back to dataframe
df = df.join(bias,on=bus_id)
return df
def get_user_offsets(df, rating, user_id, user_avg, lambda3):
overall_avg = df[rating].mean()
#top of equation
df['individualRatingMinusAverage'] = df[rating] - overall_avg #temporary column
summedDifference = df.groupby(user_id)['individualRatingMinusAverage'].sum()
df.drop('individualRatingMinusAverage',axis=1,inplace=True) #get rid of temporary column
#bottom of equation
ratingCount = df.groupby(user_id)[rating].count()
#final result
bias = pd.DataFrame(data=summedDifference / (ratingCount + lambda3),
columns=['user_bias'])
#add result back to dataframe
df = df.join(bias,on=user_id)
df['avg_review_stars'] = overall_avg
return df
Approach 2: Use Ridge regression for optimizing the bias terms¶
def cv_optimize(clf, parameters, Xtrain, ytrain, n_folds=5, scoring=None):
if not scoring:
gs = GridSearchCV(clf, param_grid=parameters, cv=n_folds)
else:
gs = GridSearchCV(clf, param_grid=parameters, cv=n_folds, scoring=scoring)
gs.fit(Xtrain, ytrain)
return gs
def cv_optimize_with_sets(clf, parameters, sets, model_name, param_name, n_folds=5, scoring=None):
Xtrain, Xtest = sets['X_train_sparse'], sets['X_test_sparse']
ytrain, ytest = sets['y_train'], sets['y_test']
gs = cv_optimize(clf, parameters, Xtrain, ytrain, n_folds=n_folds, scoring=scoring)
limit_values = np.vectorize(boundaries_stars)
ytrain_hat = limit_values(gs.predict(Xtrain))
ytest_hat = limit_values(gs.predict(Xtest))
# R2
train_r2 = r2_score(ytrain, ytrain_hat)
test_r2 = r2_score(ytest, ytest_hat)
# RMSE
train_RMSE = np.sqrt(mean_squared_error(ytrain, ytrain_hat))
test_RMSE = np.sqrt(mean_squared_error(ytest, ytest_hat))
print("""{}. Best parameter: {}={}.
Train R2:{:2.2f}% Test R2:{:2.2f}%
Train RMSE: {:0.3f}. Test RSME: {:0.3f}""".format(
model_name, param_name, gs.best_params_[param_name],
train_r2, test_r2, train_RMSE, test_RMSE))
return gs, gs.best_params_[param_name], train_r2, test_r2, train_RMSE, test_RMSE
Step2_Option1_Results_DF = pd.DataFrame(Step2_Option1_CV_Results)
print(Step2_Option1_Results_DF.loc['test_RMSE',:].idxmin())
sets={}
sample_train, sample_test = train_test_split(sample_df[sample_ftres_dummy + ['review_stars']], test_size=0.25, random_state=777)
sets['bsln'] = create_set(sample_train, sample_test, 'review_stars', sample_ftres_dummy, [5,6])
Step2_Option1_Final_Results = create_optimal_model(df=sample_df, ftres_all=sample_ftres_dummy, response=['review_stars'],
rating='review_stars', bus_id='business_id', bus_avg='stars',
user_id='user_id', user_avg='user_average_stars',lambda2=30,lambda3=45)
Step2_Option1_Final_Results['test_RMSE']
Approach 2 results:¶
alphas = [1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 0, 1, 1e2,1e3, 1e4, 1e5]
ridge = Ridge(fit_intercept=False)
gs, blsn2_alpha,train_r2, test_r2,train_RMSE, test_RMSE = cv_optimize_with_sets(ridge, {"alpha": alphas},
sets['bsln'], "Ridge Linear Regr Model",
"alpha", n_folds=5,
scoring="neg_mean_squared_error")
We see that our first method of regularization (regularizing by introducing a lambda term in the demoniator) gives us a better RMSE score than using the Ridge method of regularization.¶
Memory-Based Collaborative Filtering¶
# Prior to applying memory-based collaborative filtering, we first organized the data into a dataframe
# where each row is a pair of user and restaurant review rating.
df.head()
Using the above dataframe, we created user-item matrix for performing memory-based collaborative filtering. In the user-item matrix, one axis represents the users, and another axis being the restaurants. Each value in the matrix will represent the rating for that user and restaurant.
"""
create_matrix()
-transforms a dataframe into a user-item matrix
inputs: dataframe, number of users, number of items
outputs: user-item matrix
"""
def create_matrix(df, n_users, n_items):
matrix = np.zeros((n_users,n_items))
for line in df.itertuples():
matrix[line[1]-1, line[2]-1] = line[3]
return matrix
The dimensions of the matrices are (n_users * n_items). This causes the matrix to be quite large. Because the large size of the data is computationally too costly, we decided to use a random sample of the entire data set.
train, test = cv.train_test_split(df, test_size=0.25) #split dataframe into train/test
sample_train, sample_test = cv.train_test_split(sample_df, test_size=0.25)
train_matrix = create_matrix(train, n_users, n_items)
test_matrix = create_matrix(test, n_users, n_items)
sample_train_matrix = create_matrix(sample_train, sample_n_users, sample_n_items)
sample_test_matrix = create_matrix(sample_test, sample_n_users, sample_n_items)
print(train_matrix.shape)
print(sample_train_matrix.shape)
Using the user-item matrix (sample data, not the entire set), we computed the item-item similarity and user-item similarity. Since the ratings are all positive, the output will range from 0 to 1.
- Item-Item collaborative filtering: "Users who liked this restaurant also liked ..."
- User-Item collaborative filtering: "Users who are similar to you also liked ..."
sample_user_similarity = pairwise_distances(sample_train_matrix, metric='cosine')
sample_item_similarity = pairwise_distances(sample_train_matrix.T, metric='cosine')
Next is to use our similarity matrices to make predictions. We will need to consider bias again when comparing user-similarity. This is not necessary for item-similarity, because each user is used in the prediction itself. Also, we created a training matrix with 75% of the observations, and a test matrix with 25% of the observations.
"""
memory_based_prediction()
-uses the cosine similarity to make predictions for user-item ratings
inputs: ratings matrix, cosine similarity, flag to account for biases
outputs: predictions for user-item ratings
"""
def memory_based_prediction(ratings, similarity, bias=False):
if bias: #account for biases for users
mean_user_rating = ratings.mean(axis=1)
bias = (ratings-mean_user_rating[:,np.newaxis])
prediction = mean_user_rating[:,np.newaxis] + similarity.dot(bias) / np.array([np.abs(similarity).sum(axis=1)]).T
else:
prediction = ratings.dot(similarity) / np.array([np.abs(similarity).sum(axis=1)])
return prediction
sample_item_prediction = memory_based_prediction(sample_train_matrix, sample_item_similarity)
sample_user_prediction = memory_based_prediction(sample_train_matrix, sample_user_similarity, bias=True)
We see that the user-based prediction model is slightly more accurate than the item-based prediction model.
print("user-item based collaborative filtering RMSE: ", rmse(sample_test_matrix,sample_user_prediction))
print("item-item based collaborative filtering RMSE: ", rmse(sample_test_matrix,sample_item_prediction))
Model-based Collaborative Filtering¶
Because there is not a huge overlap between all users and all restaurants, we observed that our dataframe is very sparce (>99.9%), as expected. Given this sparsity, we also implemented model-based CF that is able to deal with sparsity better than memory-based CF.
sparsity=round(1.0-len(df)/float(n_users*n_items),10)
print("percent sparsity = ", sparsity)
"""
SVD_prediction()
-uses singular value decomposition to make rating predictions
inputs: matrix, number of singular values and vectors to compute
output: prediction through SVD
"""
def SVD_prediction(matrix, k_size):
u, s, vt = svds(matrix, k = k_size) #create matrices described above
s_diag_matrix=np.diag(s) #take diagonal matrix of S
prediction = np.dot(np.dot(u, s_diag_matrix),vt) #prediction is the dot product of u, s, and vt
return prediction
Since it is not known how many latent (singular) vectors we should use for the model, we decided to use cross validation to choose the optimal K.
"""
cross_validate_k
-uses cross validation to determine the optimal K size for the SVD_prediction() function
inputs: dataframe, list of k sizes to use, amount of folds to use in cross-validation
outputs: dictionary of train RMSE values and test RMSE values for each size of k
"""
def cross_validate_k(df, k_list, nfolds):
scoreDict = {}
for k_size in k_list:
train_RMSE_list = []
val_RMSE_list = []
for f_train, f_val in KFold(n_splits=nfolds,shuffle=True,random_state=9001).split(df.index):
train_matrix = create_matrix(df.iloc[f_train], n_users, n_items)
val_matrix = create_matrix(df.iloc[f_val], n_users, n_items)
X_pred = SVD_prediction(train_matrix, k_size)
train_RMSE = rmse(X_pred, train_matrix)
val_RMSE = rmse(X_pred, val_matrix)
train_RMSE_list.append(train_RMSE)
val_RMSE_list.append(val_RMSE)
scoreDict[k_size] = [np.mean(train_RMSE_list),np.mean(val_RMSE_list)]
return scoreDict
We will use our sample dataset to cross-validate K, since the process is very computationally expensive.
k_list = [1,5,10,20,50,100]
svd_score_dict = cross_validate_k(df=sample_train,
k_list=k_list,
nfolds=5)
sns.set_context('poster')
sns.set_style('whitegrid')
fig, ax = plt.subplots(1, 1 ,figsize=(5,5))
ax.plot(svd_df['k'], svd_df['Train'], label='train')
ax.plot(svd_df['k'], svd_df['Validation'], label='validation')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set_xlabel('Size of K')
ax.set_ylabel('RMSE')
plt.show()
We see that as k increases, the training RMSE decreases while the validation RMSE increases. This might look like the model is getting overfitted as k is increasing. However, the actual reason is that the model is able to make a greater number of predictions with a larger k, thus the overall error is larger. Furthermore, the difference in RMSE is only about 0.01, so even at the "worst" RMSE at k=30, the model-based CF is performing much better than the memory-based CF and the baseline model.
# to illustrate that the number of predictions is increasing with a greater k:
sizeDict = {}
for k in k_list:
sizeDict[k] = (SVD_prediction(sample_train_matrix, k).flatten() >=1).sum()
fig, ax = plt.subplots(1, 1 ,figsize=(5,5))
ax.plot(size_df['k'], size_df['Total Count of Predictions'])
ax.set_xlabel('Size of K')
ax.set_ylabel('Total Predictions Made')
plt.show()
RMSE of model-based CF:¶
Unfortunately the full prediction matrix is too large to report the RMSE score. As a result, we report the sample RMSE score as a reference. We would expect the overall RMSE to be somewhat similar.
X_pred = SVD_prediction(train_matrix, 100)
sample_X_pred = SVD_prediction(sample_train_matrix, 100)
print(rmse(sample_X_pred, sample_test_matrix))
Results¶
Even though we can't report the RMSE score, we can still use the results from this prediction matrix to make recommendations. However, this SVD method is still unable to make predictions for certain users, as we will demonstrate below. But first, we filtered the data so that we won't recommend restaurants that a user has already been to.
# filter the data to get rid of restaurants that a user has been to already
entire_matrix = create_matrix(df, n_users, n_items)
We also only want to recommend restaurants that we predict the user will like. The challenge with this is for users that do not have many ratings. If a user only has 2 ratings, for example, that is not enough information to determine what types of restaurants that user likes.
As a result, we will use any predictions from the SVD model if the user has less than 10 total ratings. If the user has more than 10 total ratings, we will only make recommendations from the SVD model if we predict that the given restaurant will be rated higher than that user's average.
If we are unable to make at least 3 recommendations using these methods, we will add additional recommendations by looking at that user's highest rated restaurant, then using k-nearest neighbors with cosine similarity to find the most similar restaurants.
First, we determined how many users will be given recommendations based on the model-based CF prediction.
def user_prediction_count(model,n_users):
prediction_count=0
user=0
while user <= n_users:
#figure out which users the restaurant has already rated
restaurants_rated = entire_matrix[user,:].nonzero()
if user_rating_count[user] <= 10:#if the user has less than 10 ratings, we will use any predictions from the SVD model
mask = X_pred[user,:] >= 1.0 #a predicted rating of less than 1.0 means we have an invalid prediction
else:#if the user has 10 ratings, we will only recommend restaurants that have a predicted rating higher than the user's average
mask = X_pred[user,:] >= user_id_key_rating[user]
restaurant_predictions = np.where(mask)
#remove already-rated restaurants from possible restaurant recommendations
recommendations = np.setdiff1d(restaurant_predictions,restaurants_rated)
#return recommendations.shape[0]
if recommendations.shape[0] >=1:
prediction_count+=1
user+=1
return prediction_count
user_prediction_count(X_pred,10000)
Out of 10,000 users, our model is able to make SVD recommendations for ~10%. As a result, we expect 90% of recommendations to come from k-nn using cosine similarity.
Recall that cosine similarity is not scalable. As a result, we will calculate k-nn using the sample dataset. However, since we are not using this k-nn to fit a model, we can combine our training and test set to increase the size of the matrix.
sample_entire_matrix = create_matrix(sample_df,sample_n_users, sample_n_items)
sample_entire_item_similarity = pairwise_distances(sample_entire_matrix.T, metric='cosine')
"""
similar_businesses()
-function essentially works as a k-NN function using the pairwise distance matrix
-this function filters out non-ratings by filtering out any cosine similarities of 1.0. The idea is that
a similarity of 1.0 is highly unlikely unless it is as a result of pure non-ratings. The sophistication of this function would
be an area of improvement if we had more time on this assignment
inputs: list of businesses,
"""
def similar_businesses(businesses,similarity_matrix,k):
closest = np.zeros((n_items,k))
for business in businesses:
all_businesses = similarity_matrix[business,:]
mask = all_businesses < 1
closest[business]=np.where(mask, all_businesses, np.nanmin(all_businesses)).argsort()[-k:][::-1]
return closest
business_similarity_matrix = similar_businesses(sample_df['business_id_key'].unique(),sample_entire_item_similarity,3)
business_similarity_matrix
Now we are ready to make our final function
def restaurant_recommender(user):
#figure out which users the restaurant has already rated
restaurants_rated = entire_matrix[user,:].nonzero()
if user_rating_count[user] <= 10:#if the user has less than 10 ratings, we will use any predictions from the SVD model
mask = X_pred[user,:] >= 1.0 #a predicted rating of less than 1.0 means we have an invalid prediction
else:#if the user has 10 ratings, we will only recommend restaurants that have a predicted rating higher than the user's average
mask = X_pred[user,:] >= user_id_key_rating[user]
restaurant_predictions = np.where(mask)
#remove already-rated restaurants from possible restaurant recommendations
recommendations = np.setdiff1d(restaurant_predictions,restaurants_rated)
n_SVD_recommendations = recommendations.shape[0]
if n_SVD_recommendations >=3: #if we can give 3 recommendations from SVD, we will do that
listOfIndices = list(recommendations)
top3Indices = X_pred[user,recommendations].argsort()[-3:][::-1]
final_recommendation = [listOfIndices[i] for i in top3Indices]
#last, we convert the business_id_key to the business name
return list(business_id_key_name[final_recommendation].values)
elif n_SVD_recommendations >=1: #if we can't give 3 recommendations, but can give 1, that will be our first recommendation
listOfIndices = list(recommendations)
top_n_Indices = X_pred[user,recommendations].argsort()[-n_SVD_recommendations:][::-1]
final_recommendation = [listOfIndices[i] for i in top_n_Indices]
else: #if no SVD predictions, create an empty list to append to
final_recommendation = []
#find restaurants similar to that user's highest rated restaurant
highest_rated_restaurant = user_highest_rated_restaurant[user]
similar_to_highest_rated = list(business_similarity_matrix[highest_rated_restaurant].astype(int))
#add these similar restaurants to the recommendation list until we have 3 total recommendations
for i in range(3-n_SVD_recommendations):
final_recommendation.append(similar_to_highest_rated[i])
#last, we convert the business_id_key to the business name
return list(business_id_key_name[final_recommendation].values)
# for user no. 6
restaurant_recommender(6)
# for user no. 6000
restaurant_recommender(6000)
# for user no. 60000
restaurant_recommender(60000)
Conclusions and Future Work¶
Between all of the models tested, SVD had the best score when using the RMSE metric (baseline: 1.2; memory CF: 3.9; model-based CF (SVD): 0.04). The drawback to SVD is that it only makes predictions for ~10% of users, meaning that an ensemble method is required to make predictions using an SVD model. Another drawback to our SVD model is that it just makes a prediction; there are no coefficients, which makes interpretability of features difficult.
If given more time, we would revisit the cosine similarity functions. It seems that these functions failed because there are such a large amount of users. If we were able to filter to a subset of the most important users for any given business, we would be able to reduce the size of this matrix and make a more accurate similarity model as a result. However, this approach would be limited to only those users who are active in Yelp.
The results from our regularized regression could also likely be improved if we spent more time determining what the most important categorical features were. Lastly, another avenue for improvement would be to incorporate the regularized user bias and restaurant bias into our collaborative filtering models so that it increases the interpretability and the number of predictable users. Such hybrid approach would also address the cold-start problem. Our EDA work clearly showed that there are relationships between restaurant attributes, thus it would be a great addition to the CF models to improve predictability.